X-LABO: 斜面への衝突判定と反射2

斜面への衝突判定と反射2

画面各点を次のように定義します。

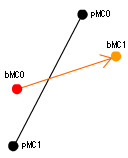
bMC0 : 赤い点を示すムービークリップ
bMC1 : オレンジ点を示すムービークリップ
pMC0 : 黒点を示すムービークリップ
pMC1 : 黒点を示すムービークリップ

■図2

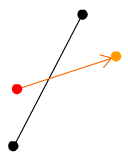
最初にボールが斜面に衝突しているかどうかの判定を行います。ボール移動前の赤い点とボール移動後のオレンジ点を繋ぐオレンジの線が斜面の線に交差している場合、ボールが斜面に衝突したことを意味します。

まずは二直線が交差しているかどうかを調べる方法は以下のサイトが参考になりました。
http://hp.vector.co.jp/authors/VA033460/tips/001.html
一番下にソースコードがあるので、これを利用させていただくことにします。但し、ソースはＣ言語用のものなのでFlash用に修正したものは↓こちらです。

Equation.checkCrossingメソッド

trueが返った場合次の処理に移ります。

■図3

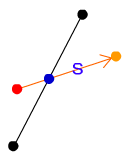
線が交差していた場合、線と線との交点を求めます。交点を求めることにより斜面にめりこんでしまった距離Ｓを求めることができます。
線と線との交点を求める方法は、以前のエントリー

交差する直線の交点の座標を求める

で作成したEquation.crossPointメソッドを利用します。

Equation.crossPointメソッド

線と線との交点の座標が求まったら、ボールが斜面にめりこんだ移動量Ｓを取得します。
三平方の定理を使用してもめりこんだ量Ｓは求まりますが、Flash8から利用できるPointクラスのdistanceメソッドを用いても求めることができるようなので、Pointクラスを利用してみることにします。

ここまでのソース

//各ポイント設定
var obj1:Object = { x1:this.pMC0._x, y1:this.pMC0._y, 
					x2:this.pMC1._x, y2:this.pMC1._y };
var obj2:Object = { x1:this.bMC0._x, y1:this.bMC0._y, 
					x2:this.bMC1._x, y2:this.bMC1._y };
					 
//二直線が交差していない場合終了
if( Equation.checkCrossing( obj1, obj2 ) == false ){ return; }
	
//交点の座標データ取得	
var cls:Object = Equation.crossPoint( obj1, obj2 );

//めりこんでいる移動量を取得
var S:Number = Point.distance( new Point( sc.cls.x, sc.cls.y ),
						  new Point( this.bMC1._x, this.bMC1._y ) );

■図6

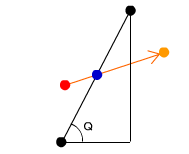
斜面を水平にするため、角度Ｑを求めます。

var Q:Number = Math.atan(
	( this.pMC0._y-this.pMC1._y ) / ( this.pMC0._x-this.pMC1._x ) );

この式で求まるのは角度ではなくラジアンです。ラジアンに関しましては以下のサイトが参考になります。

http://www.procreo.jp/tutorial03.html
http://www.macromedia.com/jp/support/flash/ts/documents/fl0189.html

■図7・図8

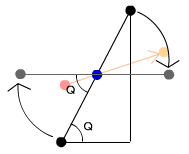
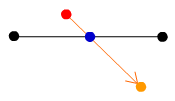
赤い点を青い点を原点としてＱだけ回転させます。図ではわかりやすくするため全ての点を回転させていますが、実際は赤い点のみを回転するだけで済みます。

Flash8から使用可能なMatrixクラスのrotateメソッドを利用すれば、座標回転が行えるようですが、ヘルプを見てみたところパラメータの設定方法がちょっとよくわからなかったため、座標回転用公式を用いることにします。↓参考サイトです。

http://www.geisya.or.jp/~mwm48961/kou2/linear_image3.html

ｘ’＝ｘcosθ-ysinθ
ｙ’＝ｘsinθ+ycosθ

この式を利用し、専用のメソッドを用意します。(メソッドにする必要はないかも…)

//指定座標を指定ラジアン分回転
private function rotate( x:Number, y:Number, rad:Number ):Object{
	
	return { x:x*Math.cos( rad ) - y*Math.sin( rad ), 
			 y:x*Math.sin( rad ) + y*Math.cos( rad ) };
}

//青点を原点として赤点を回転
var obj3:Object = rotate( bMC0._x - cls.x, bMC0._y - cls.y, -Q );
var ax:Number = obj3.x;
var ay:Number = obj3.y;

■図9

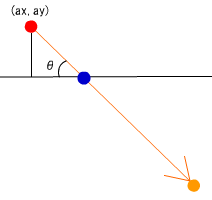
上記コードにより赤点座標(ax,ay)が求まりました。

次に赤点の斜面への入射角θ(st)と反射角θ(qt)を求めます。

var st:Number = Math.atan2( ay, ax );
var qt:Number = ( st < 0 ) ? ( -Math.PI-st ) : ( Math.PI-st );

得られたstは角度に直すと-180～180までの間の値となります。stの符号の正負によって反射角qtの正負を調整する必要があります。

Math.atanメソッドとmath.atan2メソッドの違いは先ほどのマクロメディアの参考サイトに書かれています。最初は？な感じでしたがじっくり読んでサンプルコードを作成し色々試してみてようやく理解できるようになりました。

http://www.macromedia.com/jp/support/flash/ts/documents/fl0189.html

■図10

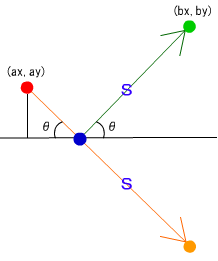
移動量Ｓと反射角θ(qt)を用いて緑点の座標(bx,by)を求めます。sinとcosを用いて求めてもいいですが、Flash8より使用可能なPointクラスのpolarメソッドを用いることにより、(bx,by)の座標を求めることができるようです。

var pnt:Point = Point.polar( S, qt );
var bx = pnt.x;
var by = pnt.y;

■図11

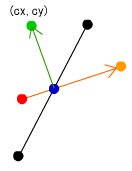
青点を原点とし、(bx,by)をＱだけ元に回転しなおします。すると、求めたい座標(cx,cy)が求まります。

var obj4:Object = rotate( bx, by, Q );
var cx:Number = obj4.x + cls.x;
var cy:Number = obj4.y + cls.y;

ここまでで、ボールの反射位置についての処理は完成です。

■図12

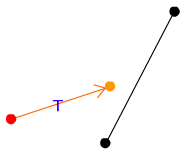
反射後の移動量調整処理を行います。
まず、ボール移動量Ｔは最初に確保しておきます。

//ボール移動用変数
var x   :Number = 2; //X軸移動量
var y   :Number = 2; //Y軸移動量
var xvec:Number =1;  //X軸移動方向 1 or -1
var yvec:Number =1;  //Y軸移動方向
var T   :Number = Math.sqrt( x*x + y*y ); //移動量

■図13

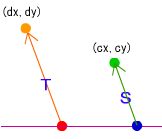
反射後のX軸Y軸から、移動方向を取得します。
また、反射後のボールのX軸とY軸の移動量(dx,dy)を求めます。

S:T = cx:dx
S:T = cy:dy

dx = T*cx/S;
dy = T*cy/S;

//反射位置より反射後の移動方向取得
xvec = ( cx > cls.x ) ? (1) : (-1);
yvec = ( cy > cls.y ) ? (1) : (-1);

//次からの移動量を設定
dx = T * Math.abs( cx ) / S;	
dy = T * Math.abs( cy ) / S;	
x = dx;
y = dy;

移動量を求めるので、(cs,cy)の値は絶対値にしています。

以上のコードを繋げれば斜面への衝突判定と反射を実現できます。衝突対象の物体はボールと表現しましたが、今回の例ではボールの中心点をとって計算しているので、点と斜面との衝突判定ということになります。実際斜面とボールとの衝突判定を行う場合は、ボールの外周も意識する必要があります。

役に立った参考サイト
ベクトル
 内積の意味(今回は内積は使用しませんでした)
ベクトルで当たり判定をとる

ボールの反射
 プログラマールーム三角形の当たり判定

[ FLASH ] [ tips ] 投稿者 siratama : 2005年11月13日 16:39