斜面への衝突判定と反射1
斜面への衝突判定と反射1
ついにねんがんの物体斜面衝突反射判定方法をてにいれたぞ!
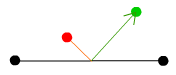
左図のような真っ直ぐな面にボールがぶつかった時の衝突判定と反射方法は簡単に実現可能です。
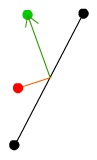
しかし右図のような斜面にボールがぶつかった場合の衝突判定と反射方法はどのようにしたら求めることができるのかなあと以前から悩んでおり、自分の中の課題の一つとなっていました。
今回三日ほど山に篭って頭を沸騰させた結果、なんとか実現方法への解を導き出せたので以下にその手順を記します。
成果物はこちら。
黒い点はドラッグ&ドロップして移動することが可能です。斜面にぶつかったボールが等角に反射できている事が確認できると思います。
まずは図による考え方から記します。
我流で考えた方法故、途中とても無駄な処理がある恐れがあります。変な箇所がありましたら突っ込みください。
※数学・物理など昔学校でならった知識はほぼ忘れている人間が書いています。
■図1
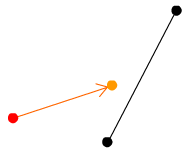
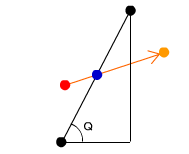
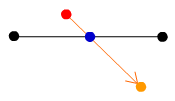
まず赤い点が一フレーム内でのボールの移動前の座標。オレンジ色の点が一フレーム内でのボールの移動後の座標とします。黒い二つの点の間に引かれた線が、衝突判定対象の斜面を示します。ボールは右上方向に進んでいます。
■図2
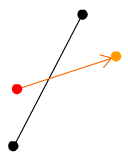
次のフレーム、ボールが移動して赤い点とオレンジ点の間の線がが黒線に交差しました。この時、斜面にボールがぶつかっていることになります。
■図3
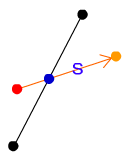
ここで、線が交差した場所に青い点を記します。青い点はボールが反射する座標になります。青い点からオレンジ色の点までの距離Sがボールが斜面にめりこんでしまった移動量です。
■図4・図5
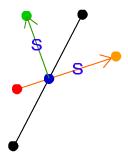
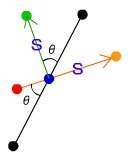
ボールが反射する位置はだいたい緑色の点の位置当たりだろうと想像がつきます。この緑の点は、赤い点が黒の斜面に入射した角と等しく反射することもわかると思います。黒の斜面から見て赤い点の入射角がθならば緑の点の反射角もθになります。
緑の点が最終的に求めたい座標なので、この座標を求める方法を考えます。
■図6・図7
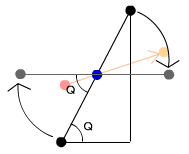
一度緑の点を忘れ、ボールの反射点である青い点を原点として、黒の斜面が水平になるように画面各点を回転させます。(実際に回転する必要のある点は赤い点の座標だけでいいのですが、説明をわかりやすくするため画面各点全てを回転させます。)
黒の斜面を水平になるまで回転する角度はQとなります。
■図8
青い点を原点とし回転させると各点はこのようになります。各座標を指定角度回転させる方法は↓こちらのページを参考に。今は図による説明なので見なくても大丈夫です。
http://www.geisya.or.jp/~mwm48961/kou2/linear_image3.html
■図9
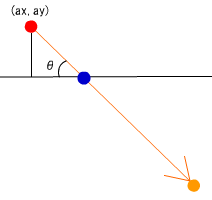
図が小さく少し見にくいので少し拡大して表示します。
回転前の赤い点を角度Qだけ回転した座標が(ax,ay)となります。座標(ax,ay)よりタンジェント(tan)を用いることにより赤点の斜面に対する入射角θが求まります。
■図10
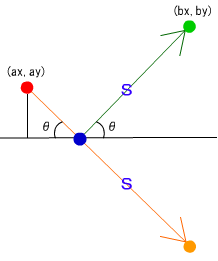
青点からオレンジ点までの移動量Sは斜面にめりこんだ量であり、反射後の移動量にもなります。移動量Sと入射角θを用いると緑の点の座標(bx,by)が求まります。
cosθ = bx/S
sinθ = by/S
bx = S * cosθ
by = S * sinθ
■図11
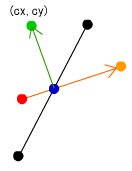
緑の点の座標が求まりましたので、先ほど画面各点を回転した分Qだけ元に回転させて、各点を元の座標に戻します。(実際は緑の点の座標を回転させるだけで済みます。)
(bx,by)をQだけ元に回転した座標が(cx,cy)となります。この(cx,cy)がボールが反射した所の座標を示します。次フレームに、(cx,cy)へボールの位置を設定してやればボールが跳ね返って見えるという寸法です。
[ 反射後の処理 ]
ボールの反射する座標は求まりましたが、まだすべき作業があります。反射した後のボールのX軸Y軸の移動する量について考えなくてはいけません。
例えば今までボールは一フレーム毎に X軸に2ピクセル Y軸に2ピクセル進んでいたとします。水平な面に衝突した場合、Y軸の移動ピクセルを反転して-2にすれば、ボールは反転後の移動量を求めたことになります。
しかし斜面に衝突したボールは 反射したボールの角度に応じてX軸Y軸の移動量を調節しなくてはなりません。
■図12
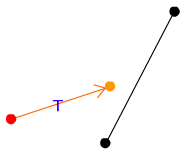
まず、あらかじめボールの一フレームに対する移動量Tを求めておきます。移動量Tは三平方の定理で求まります。
■図13
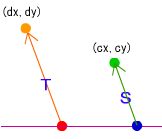
次に先ほど求めた緑の点の移動量SとXとYの移動量(cx,cy)から、反射後のボールのXとYの移動量(dx,dy)を求めます。
S:T = cx:dx
S:T = cy:dy
dx = T*cs/S;
dy = T*cy/S;
ボール反射後、dxとdyを次のボールの移動量に設定すれば完了です。
以上で図による説明は終了です。スクリプト解説は次へ続く。
→斜面への衝突判定と反射2